Светът в една песъчинка: удивителната геометрия на Джон Наш

Джон Форбс Наш загива трагично в катастрофа на 23 май тази година. Много хора отдадоха почит към великия математик, който е популяризиран от биографията за него, написана от Силвия Насар – „Красив ум“ (A Beautiful Mind) и последвалия едноименен филм, който е базиран на книгата, пише ScienceАlert.

Една от най-обсъжданите работи на Наш е теорията на игрите. Но не толкова обсъждани са другите му математически постижения. Много математици, които разбират работата на Наш, могат да се съгласят, че той е правил други, още по-забележителни открития, освен теорията на игрите, въпреки че тя има най-голямо въздействие върху останалите области.

Освен по теорията на игрите Наш работил и в много други области на математиката, като алгебрична геометрия, топология, частични диференциални уравнения и криптография. Но може би най-впечатляващите резултати на Наш са в геометрията. За да отдадем почит към великия математик, ще се опитаме да ви покажем част от постиженията му.

Джон Наш и чистата математика

 Голяма част от работата на Наш се е свързвала с геометрията. Но с диференциалната геометрия – тя е много различни от тази, която се учи в училищата. Не се занимава с тригонометрия или Питагоровата теорема, а фокусът ѝ е върху повърхности, кривини и гладкост.

Наш, като всички математици, доказвал теореми – логически твърдения, строги, прецизни и напълно истинни, без място за неяснота. Светът на чистата математика често е суров и неразбираем, но твърденията в тази наука са абсолютни и вечни.

Е, поне на теория. Пробивите в чистата математика често стигат крайните лимити на човешкото разбиране. Дори при хората в областта отнема време, докато напълно осмислят развитието.

Работата на Наш е екстремен случай. Представял трудовете си хаотично, били трудни за проследяване, а в подхода си към математическите проблеми нямал аналог в досегашния свят. В изобретателността си приличал на нещо от друг свят. Екстравагантните методи на Наш се проявили най-вече в геометрия.

Геометрията на Наш

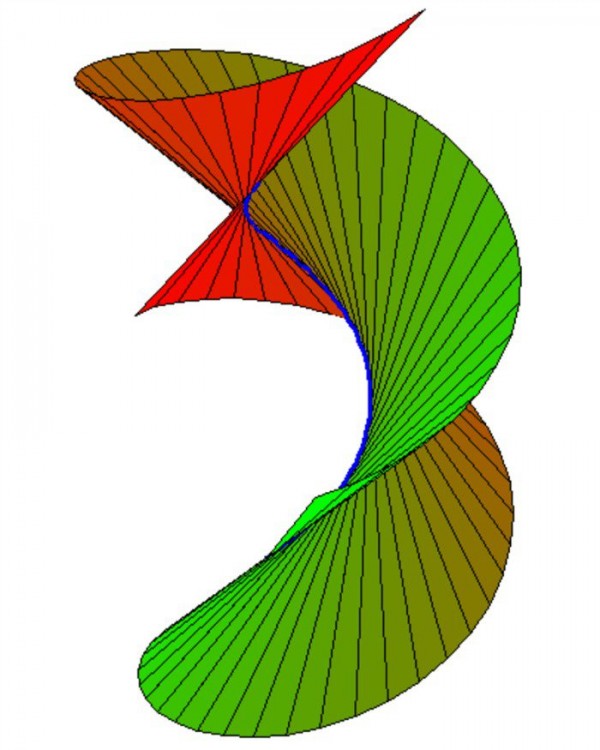
 Вземете едно парче хартия. Можете да го огъвате, но не можете да го късате или мачкате. Какви форми можете да направите? Не можете да направите сфера, или дори полусфера, защото сферата е извита, а листът хартия е плосък.

Но можете да направите цилиндър. И дори конус (това се използва и за правенето на фуниите на сладоледите, както е показано отдолу). От това излиза, че цилиндърът може да изглежда извит, но той е плосък по същество. Изглежда че в кривините има много плоски повърхности.

Gotham3/imgur

Тези идеи съществуват от стотици години, но Наш е този, който ги е развил най-много.

Задачата с вграждането

 Дошла му идеята за „вграждане” на повърхност – поставянето й в пространството без накъсване, пресичане или намачкване. Вграждане, което не деформира изначалната геометрия на повърхността, се нарича изометрично. С други думи, повърхностите долу (изображението) са „изометрични вграждания” на равнина в триизмерно пространство.

Richard Morris/Wikipedia

Задачата с изометричното вграждане може да бъде приложена не само за равнина, но и за всички възможни повърхности – сфера, поничка (което математиците наричат тор(торус), за да звучат по-аристократично) и много други.

Има повърхности, които са толкова изкривени или преплетени, че те не могат да бъдат вградени в триизмерно пространство. Всъщност те дори не могат да бъдат вградени в четириизмерно пространство.

Но Наш показал, че всяка повърхност може да бъде вградена в 17-измерно пространство. Повечето измерения, не само че не правят задачата по-трудна, а точно обратното – улесняват я, давайки повече пространство за вграждане на повърхности. По-късно работата на Наш е продължена от други учени и сега знаем, че всяка повърхност може да бъде вградена в 5-измерно пространство.

Повърхностите имат само 2 измерения, а Наш се интересувал от повърхности с всякакъв брой измерения. Тези аналози на повърхности от по-високи измерения са познати като „многообразия”

Наш доказал, че винаги може да се вгради многообразие (без да се нарушава геометрията му) в пространство от някакво измерение. С това изключително важно доказателство математикът решил задачата за изометричното вграждане.

Доказателствата на Наш хвърлили в шок голяма част от математическото общество. Методите му били революционни. Великият математик Михаил Громов казва, че работата на Наш го е поразила, била „убеждаваща като да повдигнеш някой за косата. След много хвърлени усилия в опит да разбере доказателството на Наш, Громов възкликнал „Изумително, но той успя да ни повдигне за косата”.

Изометричното вграждане в действие

 Вдъхновен от работата на Наш, Громов развил свои собствени идеи. Написал и книга – известна сред математиците като неразбираема, подобно на трудовете на Наш. В тази книга Громов описва разработения от него метод, наречен „интегриране на изпъкналост”.

Този метод имал няколко предимства. Едното е, че е по-лесно да се рисуват изображения на вграждания, чрез използването на интегрирането на изпъкналостта. Преди Громов се е знаело, че изометричните вграждания съществуват и имат изключителни свойства, но е било изключително трудно да се визуализират, най-вече защото били в по-високи измерения.

През 2012 екип от френски математици създали компютърни графики на изометрични вграждания, използвайки метода на Громов. Те са изключително сложни, почти фрактални, но все пак гладки (долната снимка).

Светът в една песъчинка

 Работата на Наш върху изометричното вграждане има много аспекти и е довела до огромен брой последвали проучвания.

Един особено интересен аспект е как са конструирани изометричните вграждания. Откритията на Наш, комбинирани с последвалата работа на Николаас Кайпер, показали че стига да можете да смалите една повърхност, то ще можете и да я вградите изометрично в триизмерното пространство.

Това звучи абсурдно. Например да вземем една сфера, да кажем повърхността на тенис топка. Представете си да смалите тенис топката до радиус 1 нанометър. Наш и Кайпер показват, че чрез достатъчно „разрошване” на повърхността (но винаги гладко – без намачкване, прегъване или разкъсване) може да се получи изометрично копие на оригиналната тенис топка, което напълно се побира в този еднонанометров радиус. Този тип „разрошване” на повърхността е пресъздаден в компютърните графики на френския екип.

Французите си представили плосък квадратен лист хартия. Залепяте горната и долната части и се получава цилиндър. Сега залепяте лявата и дясната страни и се получава нещо като изкривена поничка. Но листа хартия вече е намачкан или деформиран.

Възможно ли е да се вгради в триизмерното пространство без деформиране? Наш и Кайпер казват „да”. Громов казва да се използва интегрирането на изпъкналостта. А френските математици казват „изглежда наистина е така”!

Но математическата теорема не се прилага само за тенис топки и понички – тя важи за всички многообразия във всички измерения. Всеки свят може да се съдържа в една песъчинка.

© Hevea Project

Как го е направил?

 Наш е притежавал рядката комбинация от гений и трудолюбие. Както пише Силвия Насар в биографията на Наш, той не пестял усилия в работата по математическите проблеми.

В резултат на боледуване от шизофрения, Наш започнал да вярва на теории за конспирации, включващи извънземни и други свръхестествени същества. Когато по-късно бил запитан, защо толкова интелигентен учен вярва на подобни неща, той казал, че тези идеи му щукнали по същия начин както математическите. Затова ги взел на сериозно.

Статията е написана от Даниел Матюс (Daniel Mathews), лектор по математика в университета Монаш (Monash University) в Австралия. Оригиналната публикация е в The Conversation.