Задача за отровни бонбони взриви интернет
Известният блогър Тим Ърбан е публикувал на своя сайт задача, която взриви интернет. Условията на задачата са следните: вие се разхождате в чужда градина и намирате слива. Тъкмо лапвате няколко плода, и се появява собственикът на градината. Той ви казва, че или ще ви убият за кражбата, или трябва да изядете един от три бонбона.
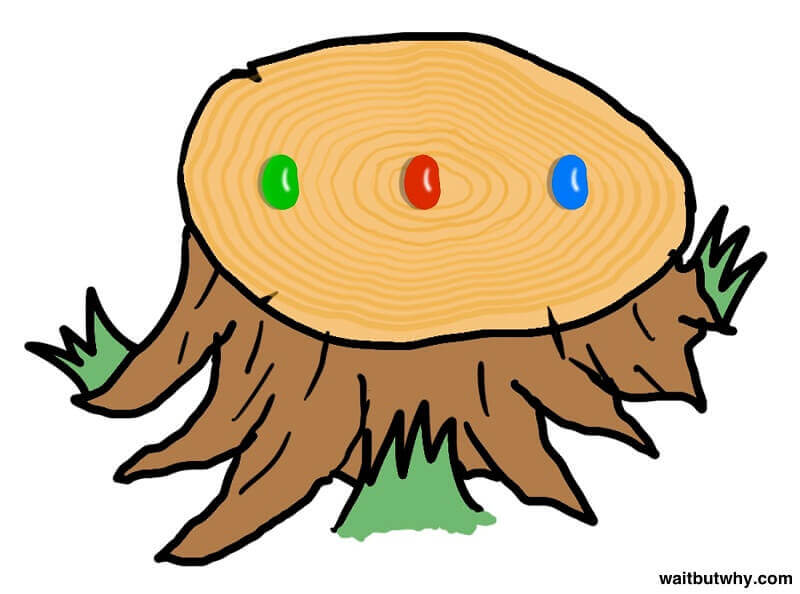
Тук виждате три бонбона – зелен, червен и син – те са поставени на пън. Два от бонбоните са отровни и ще ви убият за 30 секунди. Вие избирате зеления бонбон, вземате го в ръка и собственикът на градината ви казва, че един от отровните бонбони е синият.
Той прибира синия бонбон в джоба си. На пъна остава червеният бонбон. Въпросът е: ако премислите и не лапнете зеления бонбон, а червения, увеличават ли се вашите шансове да оцелеете?
Повечето интернет потребители са решили, че шансовете им изобщо не се увеличават. Но отговорът е друг. Става дума за следното: вероятността първоначално избраният от вас бонбон да е отровен, е 2/3. Вероятността той да не е отровен, е 1/3. И ако решите да смените зеления бонбон с червения, то имате един шанс да се отровите и два – да оцелеете.
Задачата на Тим Ърбан е препратка към парадокса Монти Хол – една от най-известните задачи от теорията на вероятностите, чието решение на пръв поглед противоречи на здравомислието. Най-разпространената формулировка на задачата звучи така:
Представете си, че сте участник в игра, в която трябва да изберете една от три врати. Зад едната от вратите се намира кола, а зад другите две – кози. Вие избирате едната от вратите, например номер 1, след това водещият, който знае къде се намира колата и къде – козите, отваря една от оставащите врати, например номер 3, зад която има коза.
След това той ви пита, искате ли да промените избора си и да изберете врата номер 2? Ще се увеличат ли шансовете ви да спечелите автомобила, ако промените своя избор?
Едно от обясненията е следното: ако промените избора на вратата след действията на водещия, то ще спечелите, ако първоначално сте избрали грешната врата. Тоест с вероятност 2/3, тъй като първоначално можете да изберете губещата врата в два случая от три.