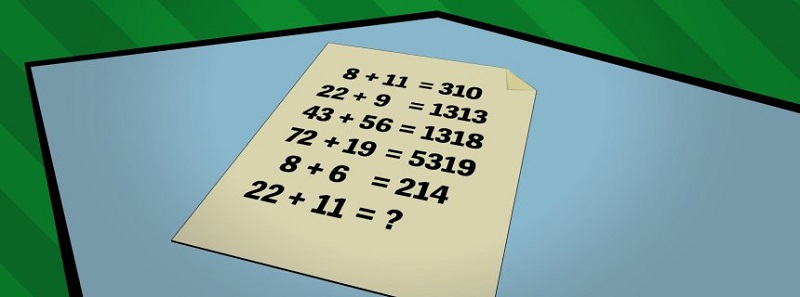На пръв поглед задачата изглежда нерешима. Има три неизвестни, които ще наречем a, b и c. Уравнението изглежда така:
a*b*c = a + b + c
Как да продължим?
Решението идва, като изясним, че произведението на три прости числа (по-големи от нула) почти винаги е по-голямо от техния сбор. Много малко са възможните решения или дори николко.
Приемаме, че „а“ е най-голямото от трите търсени числа. Следователно трябва да е вярно, че b =< a и c =< a (където =< означава по-малко или равно!). Добавяме това в първоначалното уравнение:
a*b*c = a + b + c =< 3*a
Можем да напишем също и че:
a*b*c =< 3*a
Дефинираме това неравенство чрез а и получаваме:
b*c =< 3
Знаем, че b и c са прости числа, по-големи от нула. Така стават възможни следните двойки числа за b и с:
1, 1
1, 2
1, 3
Заместваме b и с с тези числа в уравнението и получаваме като единствен възможен отговор с цели числа решението 3,2,1. Това са числата, които учениците е трябвало да умножат.
